再谈拼音匹配（二）—— 传统的字符串索引

再谈拼音匹配系列目录：
第一节 即时匹配与语境
第二节 传统的字符串索引
第三节 拼音树（上）
第四节 拼音树（下）
第五节 杂项

所有内容的实现细节参见 PinIn

前言

正如上一节结尾所说，这一节我们将会讨论传统的字符串索引。考虑到本节的核心目的只是为了后面章节的内容做一些铺垫，所以内容仍然会保持在比较浅显的水平。至于一些针对性很强的加速算法，由于他们和本项目的关系不大，我会直接跳过。

字典树

字典树（Trie）是一种极为直接的数据结构。他的核心思路就是将字符串的每个字符用作树结构的一条边。对于一个装有“amd”，“amy”，“i”和“in”四个字符串的字典树而言，它的典型结构如下：

对于不同的用途，字典树的结构可能稍有不同。图中给出的是 Set<String> 的结构。你只需要在字符串末端的节点上打一个标记（图中用红色表示），就可以完成存储。典型的前缀树通常用作 Map<String, Integer>，不同于图中的简单着色，你需要在节点中存储当前字符串对应的数值。至于 MultiMap<String, Integer>，你则需要在每个节点维护一个对应数值的集合，不过也大同小异。

压缩字典树

树结构的存储效率通常而言都算不上太高，很大程度上是因为大量的节点对象和指针。这一现象在字典树中尤为明显。对于所有基于字典树的字符串索引，一个常用的优化策略是使用树压缩。

上文提到的字典树压缩后可以得到图中的结构。因为“a”->“m”这条路径上并没有其他分支，我们可以将两条边合并为一条，从而省略中间的节点。在经过压缩之后，我们实际上将“字典树”转化成了“压缩字典树”。

当我们在优化内存占用时，一定要对对象的使用格外小心。我们再来观察一下压缩树的结构：比起原来的树，他确实少了一个节点，但是原来的树结构每条边上只需要储存一个字符，而现在则有一条边需要存储一个字符串（“am”）。这个的字符串自然又要占用额外的内存。这也就意味着，在我们削减了一部分内存开销的同时，又制造了潜在的内存消耗。在绝大部分情况下，压缩字典树（或者一个常用的变种，基数树）可以带来可观的内存优化，但是这一优势很大程度上依赖于高效的内存排布。对于一些低效率的实现，压缩树在涉及大量文本的场景中很有可能比传统字典树占用更多内存。对于压缩树的使用，我们在下一段还会继续讨论。

后缀树

前缀树对于前缀匹配的加速是不言而喻的：你只需要沿着根节点按照匹配串移动，就可以获得所有匹配该前缀的字符串。举个例子，要寻找树中所有以“am”开头的字符串，你只需要移动到节点“am”。该节点以下所有子节点对应的字符串均可匹配前缀“am”。这几乎是前缀树最为典型和广泛的使用场景。

当如果我们想要查找一个字符串能否匹配一个长串的子串（即 contains 逻辑），字典树就有些捉襟见肘了。但是，我们仍然可以基于字典树稍作改动来满足这一需求：将长串的所有后缀添加入字典树，如果有任何一个后缀满足前缀匹配，即可确认该字符串可以匹配长串的子串。这也就是所谓的后缀树。这个结构允许我们以极快的速度在极长的字符串中寻找匹配的子串。同样的，我们也可以用它来进行 DNA 序列的匹配，这就也是为什么后缀树是生物信息学上一个重要的数据结构。

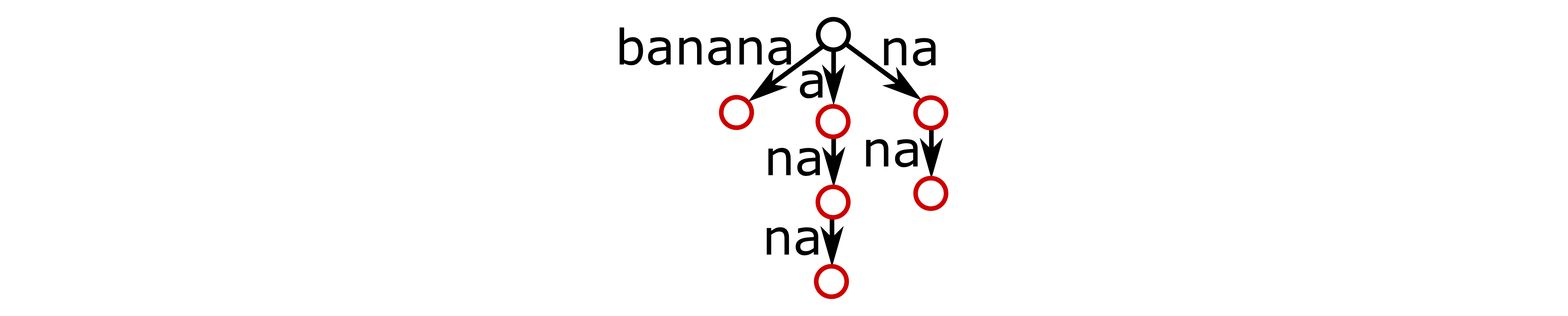
上图给出了对于“banana”的后缀树结构。本质而言，我们不过是将“banana”的所有后缀，即“banana”，“anana”，“nana”，“ana”，“na”和“a”，加入了一个压缩字典树中。如果你阅读过其他相关的文档，可能会注意到我这里用的记法和其他文档有所不同：当我们讨论后缀树时，通常使用一个字典外的字符“$”，来表示字符串结束。而我这里为了和之前的记法保持一致，用红色节点来表示，本质上并没有区别，只是看起来简洁一些。

说到这里我们重新回到压缩树的话题上，说一说为什么对于后缀树而言，使用压缩树如此重要。这里的核心就在于压缩树对于任意长的一个词条，增加的节点不会多于一个。这也就造成了一个不可忽视的差别：对于传统字典树而言，空间复杂度最坏情况下线性于文本总字符数，而对于压缩字典树而言，空间复杂度最坏情况下线性于词条数。

对于前缀匹配的场景而言，虽然压缩树的理论复杂度更好，但线性于总字符数也并非不可接受。但是对于后缀树而言，使用传统字典树对空间复杂度的影响是致命的：对于一个长度为 n 的字符串，它会产生共 n 个不同的后缀，共计 n(1+n)/2 个字符，也就是说它的空间复杂度近似线性于字符串长度的平方。而对于压缩树而言，空间复杂度仍能保持在线性于字符串长度。如果不使用压缩树，过高的空间复杂度将会使得它无法适用于绝大部分场景。

广义后缀树

后缀树固然好，但是如果只能用于单个字符串，它的应用范围就比较局限了。后缀树的能力显然不止于此。经过一些小小的改造，他就可以用于索引多个字符串的子串搜索。一个极为简单粗暴的解决方案就是将所有需要搜索的字符串拼接成一个长串，再基于这个长串构造后缀树。这一措施虽然听起来轻松，但是实际操作中需要处理相当多的边际条件和偏移量映射。为了避免这些棘手的逻辑，我们可以使用广义后缀树来建立索引。

广义后缀树不过是后缀树的一个变种。在后缀树中，我们将一个字符串的所有后缀添加到压缩字典树中，而在广义后缀树中，对于多个字符串，我们将所有字符串的所有后缀添加到压缩字典树中。为了避免混淆，不同于简单的标记字符串终点，我们不仅要标记字符串终点，还要注明是哪一个字符串的终点。这一点也可以轻松的通过前文提到的基于字典树的 Multimap<String, Integer> 来实现。

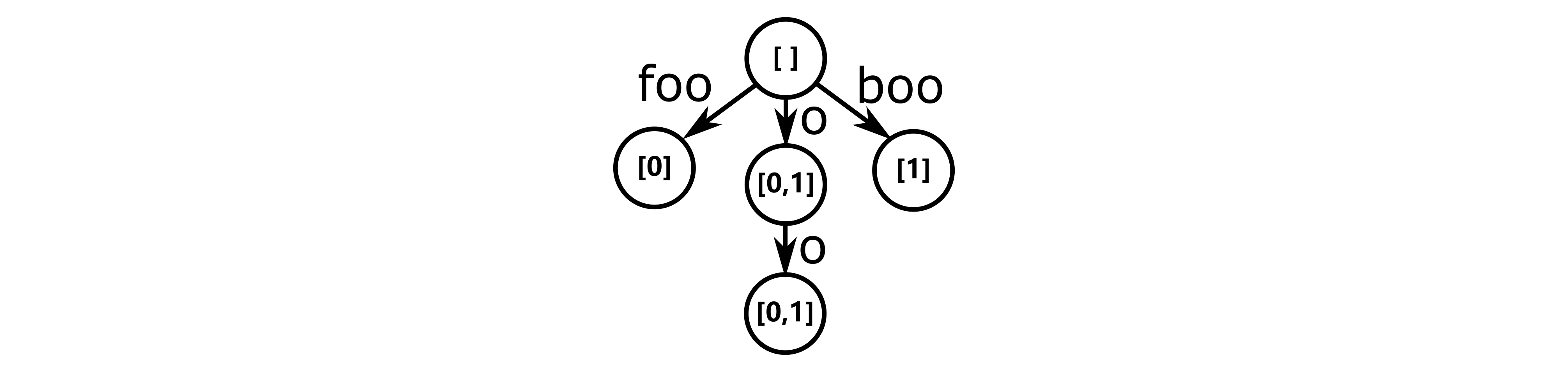
图中给出了一个简单的广义后缀树的结构，存储了“foo”和“boo”两个字符串。这里我们仍然沿用之前的记法，从而避免那些蛋疼的“$”。对于不同的字符串我们首先给他编上序号：

1
2
"foo" -> 0
"boo" -> 1

对于所有字符串的所有后缀，我们沿用上面的编号：

1
2
"foo" -> 0, "oo" -> 0, "o" -> 0
"boo" -> 1, "oo" -> 1, "o" -> 1

再将上面的所有映射关系添加到压缩字典树中，就构建了上图给出的广义后缀树。

如你所见，这个结构并不复杂，但是提供了惊人的性能：对于任意数量的字符串，在其中进行子串匹配，它的时间复杂度线性于搜索串的长度。与此同时，空间复杂度线性于字符总量。这一结构被广泛用于字符串的批量搜索，一个显而易见的例子是在游戏中使用物品的一部分名称来过滤物品。在牺牲了相当多时间建立索引，又耗费相当多内存空间存储索引之后，我们可以在毫秒内完成海量文本（上GB）的查找。

后缀数组

对于子串匹配，后缀树和广义后缀树在复杂度上近乎完美，但是我还要重申一个问题：树结构的内存使用往往并不高效。我们暂且认为一个字符在后缀树中对应一个节点，那么我们在 64 位 Java 环境下，计算一下一个节点的最小开销：

不考虑变态级别的优化技巧，基于整数范围的字符集几乎必然引入容器，这就又给每个节点增加了至少二十多字节的额外内存使用。于是我们得到这一结论：在 64 位 Java 中，对于共含有 n 个字符的文本，生成后缀树索引需要至少 50n 字节的内存。至于一些 不太谨慎的实现，内存占用甚至可以超过 200n 字节。维基上对于任何语言的一般结论是：即使是非常谨慎的实现，后缀树占用的内存基本不得少于 20n 字节。

直观地说，对于 1 MB 的文本，建立后缀树很可能需要消耗数十 MB 的内存。如果这是我们唯一的选择，我们也只能自认倒霉，但是柳暗花明，后缀数组横空出世：对于总量为 n 的文本，他只占用 4n 字节，几乎将内存消耗缩减到十分之一。

前面我们说到，树结构存储效率底下的根本原因是要储存各类节点和引用。如果我们将树结构扁平化，压缩为一个数组，就可以显著减少内存消耗。我们再回到“banana”的问题上：上图中我们给出了一个对应“banana”的后缀树。相比起之前给出的后缀树，它的子节点均按照字符顺序排列。对这个树结构前序遍历，我们就可以获得如下排列的字符串，即“banana”对应的后缀数组：

1
2
3
4
5
6
7
8
9
10
//  b a n a n a 
// 0 1 2 3 4 5 6

""       -> 6,
"a"      -> 5,
"ana"    -> 3,
"anana"  -> 1,
"banana" -> 0,
"na"     -> 4,
"nana"   -> 2

也许你已经发现，这同时也就是“banana”的所有后缀按字母表顺序排列。如果我们要对这个结构进行搜索，只需要执行两次二分查找，就可以找到对应前缀的索引范围。这个结构的另一项优势是，不同于直接存储字符串，我们可以通过存储对应后缀的索引位置来显著提高存储效率。对于上面给出的排序，我们可以直接存储箭头右侧给出的索引位置。当然这一技巧也可以用在前文所述的树结构中：通过存储起始位置和终止位置，我们可以直接表示一个字符串的切片。这也解释了为什么在前文中一个字符串被认为消耗了 8 个字节。这一技巧我们暂且称作“切片策略”，在后续章节中我们还会再次提到。

不管怎么说，后缀树组相比起树结构在存储效率上的优势是得天独厚的。他唯一的缺点就是搜索的时间复杂度稍差。对于一个 n 长的字符串，搜索一个 m 长的子串，后缀树的复杂度是 O（m）而后缀数组的复杂度是 O（m + logn）。不过在大部分情况下，logn 的部分几乎可以忽略不计。另外，这里还有 一篇论文 通过 LCP 数组将后缀数组的搜索复杂度优化到了 O（m），与后缀树相同。但是有一说一，这论文我没看明白，目前我也不想花这个时间精读。

类似于广义后缀树，通过维护一些索引的映射关系，后缀数组也可以被拓展为广义后缀数组，用于同时索引多个字符串，这也是 Minecraft 在 1.12 以及之后版本中对于物品搜索的解决方案。对于总量为 n 个字符的文本，广义后缀树的内存消耗可以轻松控制在 16n 字节以下，这对于动辄 80n 的后缀树仍然具有显而易见的优势。

小结

尽管我们在这一节并没有什么新内容，不过是将 20 年前的研究结果和大家简要的复述了一下。但是更重要的是，我们讨论了字符串索引的发展过程，分析了数据结构的设计思路，同时展示了在 O（n） 空间复杂度下对内存占用的若干次压缩以及其中的技巧。尽管他们不能直接用于拼音搜索，但是在下一节中，其中的大部分内容仍然是拼音索引的基石。这也意味着我们即将到达这段连载的核心部分，回见。

• Previous
  再谈拼音匹配（一）—— 即时匹配与语境
• Next
  再谈拼音匹配（三）—— 拼音树（上）